Point A to Point B: part 3
The problem solving continues. In part 1 we explored how to avoid objects in front of us, but not behind us. In part 2 we solved the issue of avoiding objects directly in our path.Now what's wrong? THIS:
If you look carefully, there are two characters in the way, "Mickey" and "Talan". Since the art is so bad (sorry!) it's hard to tell, but they are perfectly the same distance from Shytor's path to the enemy, Ultros.
Didn't we already solve this? Well, no. We set the algorithm to adjust for something directly in our path, but not for two items creating equal but opposing anti-gravity forces.
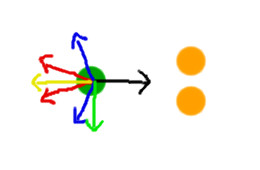
Whether we use the direct anti-gravity force vectors (red lines) or the adjusted ones (blue lines) they cancel each other out because the obstacles are exactly the same distance from the path. While this may be a rare circumstance, we have to consider the implications. When faced with multiple objects to avoid, how do we choose which way to go?
The answer was actually a bit more simple than I originally thought. All we have to do is add the original anti-gravity vectors first, and then adjust the remaining vector, as if it was one obstacle to avoid.
The yellow line represents the sum of the original anti-gravity vectors (red). The green line represents the vector after the adjustment. Obviously we choose to go to the right, because that's the side of the road you should drive on (sorry British colonies!).
Now, no matter how many obstacles there are, we end up with two vectors to make our choice: first the sum of all the adjusted vectors, and the adjusted vector of the sum of the original anti-gravity vectors. Follow?
The sum of the adjusted vectors line is not visualized in the picture above. If it was, it would be a short vector pointing in the same direction as the yellow line.
But out of those two vectors, which do we use? In this scenario, we want to use "green", but in others we might want to use our previous algorithm. Here's a basic description of how it works.
Let's call the sum of adjusted vectors "B" (sum of the blue lines above) and the adjusted sum of vectors "A" (green line above). If we add them together, we get a new vector, X. Then we find the difference between this new vector and the angle to the target: we'll call it "delta". If delta is near 180, then we want to ignore either A or B. We can defer to A or B depending on the situation, if either vector is near 180 degrees from the target angle, we want to use the other. I used the following equation to scale the deferral smoothly (it's a quarter ellipse since "delta" is less than 180 degrees). We end up with a value between 0 and 1 that is multiplied by the B vector.
In code:
if (delta != 0) igFac = Math.sqrt(1 - Math.pow(((2 * delta) - Math.PI) / Math.PI,2)); else igFac = 0; vector.vx += A.vx + (igFac*B.vx); vector.vy += A.vy + (igFac*B.vy);
It could also be a linear scale to avoid using the costly Math.sqrt() function more than necessary. However, computers are getting faster, and I like smooth transitions. The result is this:
Notice that once he makes a choice to go right, the normal algorithm takes over since both obstacles are now to his left. Problem solved! What else could go wrong?
THIS:
This particular issue was actually a simple math error, but you get the idea. Here's the code.
function moveGuy(character){
//sanity check, no movement if there is no target
if (!character.target) return;
//find the vector to the target and normalize
//then convert it to an angle in radians
//the "pos" property contains x,y coordinates
var vector = normVec(character.pos,character.target.pos);
var angle = Math.atan2(vector.vy,vector.vx);
//declarations
var d = 0;
var delta = 0;
var r = 0;
//this is the sum of the anti-gravity, yellow line
var AGSumx = 0;
var AGSumy = 0;
//this is the sum of the adjusted vectors, blue line
var AdjAGSumx = 0;
var AdjAGSumy = 0;
//"Obstacles" is a dictionary of all obstacles to avoid
for (var o in Obstacles){
if (o === character.name) continue; //skip yourself
if (o === character.target.name) continue;//skip your target
//get the distance to the obstacle
d = getDistance(character.pos,Obstacles[o].pos);
//calculate the anti-gravity magnitude
//the halo.cr property is the width with a buffer
var mass = (character.halo.cr + Obstacles[o].halo.cr);
//multiply by "personal space" constant for math fudging
//this effects the strength of the antigravity
var mass = mass * mass * 3;
var mag = mass / (d * d);
//v is anti-gravity vector (red)
var v = normVec(Obstacles[o].pos,character.pos,mag);
var av = {"vx":0,"vy":0}; //av is adjusted vector (blue)
//angle for the red lines
var vTheta = Math.atan2(v.vy,v.vx);
var obsAngle = 0;//angle to the obstacle
if (vTheta >= 0) obsAngle = vTheta - Math.PI;
else if (vTheta < 0) obsAngle = vTheta + Math.PI;
//get the difference between the angle to target and obstacle
//correct it be between -180 and 180
delta = obsAngle - angle;
if (delta > Math.PI) delta = delta - (2*Math.PI);
if (delta < -Math.PI) delta = delta + (2*Math.PI);
//magnitude of the force is scaled based on direction
r = (1 + Math.cos(delta))/2; //unit cardioid
r = r * r * r;
//get the difference between the target vector and antigravity vector
delta = vTheta - angle;
if (delta > Math.PI) delta = delta - (2*Math.PI);
if (delta < -Math.PI) delta = delta + (2*Math.PI);
//make the adjustment to get the blue lines
if (delta != 0) {
if (Math.abs(delta)>=Math.PI/2)var r2 = 1 - Math.sqrt(1 - Math.pow(((2 * Math.abs(delta)) - Math.PI) / Math.PI,2));//inverted quarter elipse
else {var r2 = 0;}// if delta > 90 else 0
var theta = Math.PI*r*r2/2;
//one method of correcting the sign if the angles are negative
var dir = Math.abs(delta)/delta;
var aTheta = vTheta - (theta * dir);
} else {
var aTheta = vTheta;
}
//convert the blue line angle to a vector
av.vx = Math.cos(aTheta)*mag;
av.vy = Math.sin(aTheta)*mag;
AGSumx += v.vx*r;//sum of red vectors (yellow)
AGSumy += v.vy*r;
AdjAGSumx += av.vx*r;//sum of blue vectors
AdjAGSumy += av.vy*r;
}//end for loop
//to fix the splitting issue, choose a direction.
//this algorithm has to choose which of the vectors to use
//so it's a bit more complex.
//basically it scales vectors to 0 based on their direction relative to the target
//magold is mag of yellow, magnew is mag of sum of blue
var magold = Math.sqrt((AGSumx*AGSumx)+(AGSumy*AGSumy));
var magnew = Math.sqrt((AdjAGSumx*AdjAGSumx)+(AdjAGSumy*AdjAGSumy));
var newx = 0;//placeholder for the adjusted anti-gravity sum (green)
var newy = 0;
//only adjust the yellow if the magnitude is greater than the sum of blue
if (magold >= magnew){
//convert the vector ratio to an angle, between 90 and 0
var newTheta = -(1-(magnew/magold))*(1/(magnew+1))*(Math.PI/2);
//find the difference between the old vector and the target vector
//is it between 90 and 180?
var oldVangle = Math.atan2(AGSumy,AGSumx);//yellow line
delta = oldVangle - angle;//diff from target vector to yellow
if (delta > Math.PI) delta = delta - (2*Math.PI);
if (delta < -Math.PI) delta = delta + (2*Math.PI);
//translate dTheta from between 90 and 180 to a ratio
if (Math.abs(delta) > Math.PI/2) {
//linear scaling
var axxx = (Math.abs(delta) - (Math.PI/2))/(Math.PI/2);
/square and give it a sign
axxx = axxx * axxx * (delta/Math.abs(delta));/
} else { axxx = 0;
}
var finalAngle = newTheta * axxx;
//calculate the adjustment, this is the green line
newx = AGSumx*Math.cos(finalAngle) - AGSumy*Math.sin(finalAngle);
newy = AGSumy*Math.cos(finalAngle) + AGSumx*Math.sin(finalAngle);
newx *= 1 - (magnew/magold);//adjust magnitude based on inverted mag ratio
newy *= 1 - (magnew/magold);
newx *= 1/(magnew + 1);
newy *= 1/(magnew + 1);
newx *= Math.abs(axxx);//if the old vector isn't near 180, don't add it
newy *= Math.abs(axxx);
}
//this scales out the sum of adjusted vectors
//first get the sum of both the adjusted vectors
var igAng = Math.atan2(newy + AdjAGSumy,newx + AdjAGSumx);
//find the difference between this combined vector and the target vector
delta = Math.abs(igAng - angle);
if (delta > Math.PI) delta = (2*Math.PI) - delta;
//if it's near 180 degrees from the target vector, we don't use it
//the sum of blue will be fine
if (delta != 0) var igFac = Math.sqrt(1 - Math.pow(((2 * delta) - Math.PI) / Math.PI,2));//quarter ellipse equation
else var igFac = 0;
//the movement vector is green vector + sum of blue vectors scaled
vector.vx += newx + (igFac*AdjAGSumx);
vector.vy += newy + (igFac*AdjAGSumy);
//normalize the vector, so it can be used for movement
vector = normalize(vector);
//set the movement vector for next frame
//then move on to the next character
character.nextmove(vector);
}
Part 4 comes with the thrilling conclusion and something I initially failed to consider at all: moving obstacles!.png)










0 comments: