.png)
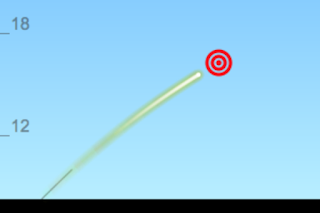
If you've ever programmed a game, then you know that physics is critical to realistic play. No, I am not going to explain how to build a physics engine. I just started with the basics. How to Launch Things Whether it is catapults, tanks or worms with slingshots, the most important thing is: whatever goes up must come down......
If you have studied physics in 3 dimensions, then you know what a pain it is to do vector math. It's abstract, it's tricky to draw on paper... So I devised a little aid. It's much easier to visualize the sum of Force and Moment (torque) vectors when you can actually turn it around, and compare at different angles....
It's been awhile so I figured: it is time for a random post. Seriously, this is a post about random numbers. If you code in Javascript, then Math.random() is probably already familiar to you. It does a nice job of generating (pretty) uniform variables from 0 to 1. A little multiplying and rounding and you can get integers from...
If the game has been too much fun for you... I kid. I'll finish it someday. Probably. In the meantime, I've been taking an Introduction to Aeronautical Engineering course on edx.org. It's a great course (and free) from Delft Technical University. If you are interested in Aerospace, start there. It'll help you determine if you like math enough... It...
In the case of my game concept, so is user input. "So what is this crazy game concept you keep talking about?" Here it is: Do you remember Super Mario RPG and timed hits? It was a fun addition to the usual turn-based RPG style game that added an extra layer of player interaction. It was a nice touch...
