Point A to Point B: part 4
We can now move fluidly around groups of objects. Amazing! On to animation and sound!Hold your horses! One more problem to solve.
What if the obstacle we want to avoid is moving? I didn't realize this was a problem until THIS happened.
Each character is heading towards a different target, and since their paths cross, they get "locked" with each other. It's a classic "who goes first?" routine.
Abbott: After you...
Costello: Right, after Yu...
Abbott: No, I insist, after you!
Costello: That's what I said. After Yu!
Abbott: After me?
Costello: No. Yu, then Mi!
Abbott: Right. Me, then you...
Costello: NO! Yu before Mi. Then Hoo.
Abbott: I don't know. Who is there?
Costello: Hoo is already here.
Abbott: Just me and you. But who is going first?
Costello: No. First Yu, then Mi, then Hoo.
Abbott: I don't know, but I'm going anyway!
Costello: You can't! Not until Yu goes.
Abbott: I'll goes when I wants to goes!
Yu: Not yet! Wait for Mi!
Abbott: Who's that?
Costello: That's Yu!
Abbott: How can he be me?
Yu: I'm not Mi. I'm YU!
Abbott: Then who am I?!
Costello: Oh, hello, Mi!
Mi: Hello, Mr. Costello!
Costello: Yu, Mi, Mr. Abbott. (introducing them)
Mi: Hello. I'm Mi. Nice to meet you!
Abbott: Well at least you know who you are! Now who are YOU?
Hoo: I am Hoo.
Abbott: That's what I asked you.
Costello: Well, we better get going. After you. (indicating Yu)
Abbott takes a step towards the door at the same time as Yu. He has to stop to let Yu go. The same happens for Mi and Hoo. Abbott glares at Costello to let him go. Neither goes.
Costello: After you...
Abbott: Just GO ALREADY!
Path Crossing and Look-ahead
This problem took a lot more forethought than the others. I decided to take each character and assess the information he has available from his own point of view. That way his decision making process will be able to mimic that of people walking around. Here's what you know:- Your own target
- Your direction and speed
- The direction and speed of the "obstacle"
What you don't necessarily know is the target of the obstacle. But this should be enough information to make a relatively informed choice. So the question is, when do we adjust our path, and when don't we.
As people, if we see someone about to cross our path, we can judge our relative speeds and make an assumption about the likelihood of a collision at the point of crossing. The farther ahead we look though, the less accurate our prediction.
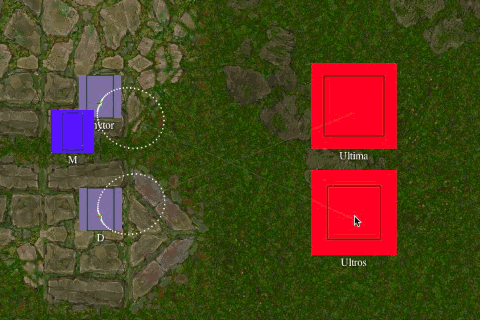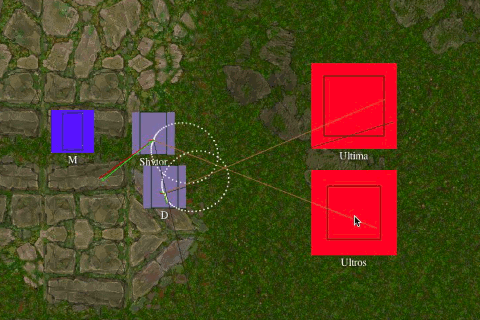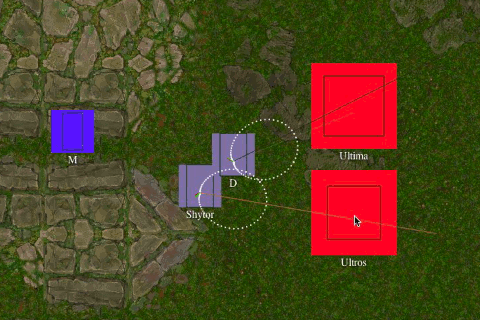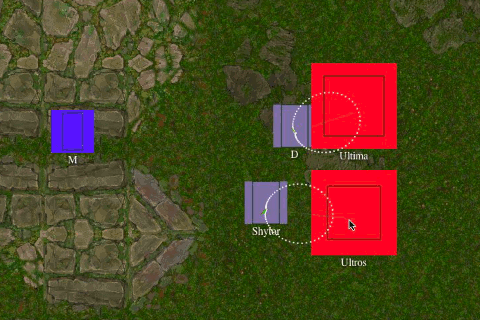
If we look ahead 40 animation frames, we can tell if our current trajectories cross, and if the obstacle's trajectory crosses our desired path to the target. By judging the speed of each object, we can tell who will hit the point of intersection first. We'll be polite and let whoever gets there first pass.
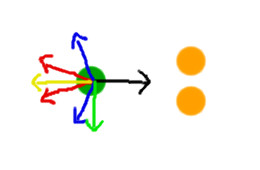
The black dashed lines indicate each object's desired path. The dotted lines represent their current trajectory. Since that is the only information BOTH parties can anticipate, we'll use it to determine who gets the right-of-way. The green dot will reach the point of intersection one frame sooner than the orange dot, so he gets to keep his current trajectory. So what do we do to adjust the direction of the orange dot?
My first thought was to have him "chase" the other, by flipping the red vector 180 degrees. That proved not to work well. Instead, I found that mirroring the red vector around the desired path as an axis got the desired result.
As you can see, by flipping the direction around the desired path as an axis (black dashes), it drastically changes his direction (red become dotted red). Keep in mind, the red vector is added back to the desired vector to produce the final direction. This works great to avoid a potential train wreck in scenarios like this. However there are some scenarios where we want to ignore a moving obstacle all together, like chasing.
Everyone loves a good chase. But if we have no chance of catching the obstacle we are following, then we might as well ignore its anti-gravity vector completely. What about a good ol' fashioned game of chicken?
Naturally we don't want a crash. Fortunately, the normal collision avoidance algorithm takes care of this. And with both objects trying to avoid each other, they do it quite effectively.
Here was my first attempt at making it all work.
Naturally, we need to scale down the adjustments as we near the time of intersection. This makes for a smooth transition out of the adjustment and back to normal collision avoidance. This is done by using ratios created with how close teach party is to the point of intersection.
There's a few bits of fancy math going on in this algorithm, starting with the calculation to find the time/point of intersect between the estimated trajectories. This handy function takes two line segments as arguments and returns the point of intersection (or false for no intersection).
function pathIntersect(p1a,p1b,p2a,p2b){
//input 4 points as arguments, 2 line segments
//returns the intersect point if they collide or false if they do not
var s1_x, s1_y, s2_x, s2_y,ix,iy;
var s1_x = p1b.x - p1a.x;
var s1_y = p1b.y - p1a.y;
var s2_x = p2b.x - p2a.x;
var s2_y = p2b.y - p2a.y;
var s = (-s1_y * (p1a.x-p2a.x) + s1_x * (p1a.y-p2a.y))/(-s2_x * s1_y + s1_x * s2_y);
var t = ( s2_x * (p1a.y-p2a.y) - s2_y * (p1a.x-p2a.x))/(-s2_x * s1_y + s1_x * s2_y);
if (s >= 0 && s <= 1 && t >= 0 && t <= 1){
// Collision detected, save the intersection point if necessary
var ix = p1a.x + (t * s1_x);
var iy = p1a.y + (t * s1_y);
return {x:ix,y:iy};
}
return false; // No collision
}
Did you notice in the last gif that the vectors turning "D" are practically pointing in the wrong direction? The adjustment I found most useful was to rotate the vectors around the path, like a mirror image. Here's the handy function for that. It mirrors mvec around vec as an axis.function mirrorVector(vec,mvec){
// mirrors mvec around vec as an axis
//get a line for vec through origin:
//y = vec.vy/vec.vx * x
//get a perpendicular line through mvec:
//y = (vec.vx/vec.vy) * x + (mvec.vy - ((vec.vx/vec.vy)*mvec.vx))
//find the intersect point
var iy = (mvec.vy + (vec.vx / vec.vy * mvec.vx)) / (1 + ((vec.vx*vec.vx)/(vec.vy*vec.vy)));
var ix = vec.vx / vec.vy * iy;
var newx = 2 * (ix - mvec.vx) + mvec.vx;
var newy = 2 * (iy - mvec.vy) + mvec.vy;
return {"vx":newx,"vy":newy};
}
In addition to these helpers, we must insert this code in the original "move" function.av.vx = Math.cos(aTheta)*mag;
av.vy = Math.sin(aTheta)*mag;
//place this code after the above lines from part 3.
////////experimental adjustment for crossing paths////////
var d40 = getVecLength(character.vel) * 40 + (character.w/2);//adjust this line!!!
// distance to obstacle must be less than velocity x 40 frames
// delta must be between -90 and 90
// other guy must be moving, not stationary
if (d < d40 && dx > -Math.PI/2 && dx < Math.PI/2 && Obstacles[o].isMoving()) {
var vv = crossPathFix(d40,d,vector,v,av,character,Obstacles[o]);
v.vx = vv.v.vx;
v.vy = vv.v.vy;
av.vx = vv.av.vx;
av.vy = vv.av.vy;
}
///////////End of experimental adjustment/////////////////
Here is the code for the fix. There are a few more helper functions at the bottom. function crossPathFix (d40,dis,vector,v,av,guy1,guy2){
//distance in 40 frames depending on current speed
//distance to path crosser
//desired vector
//angle of path crosser
//adjusted angle
//make line segments from current positions to anticipated position in 40 frames
var g1 = guy1.lookAhead(vector);
var g1v = guy1.lookAhead();
var g2 = guy2.lookAhead();
intersect = pathIntersect(g1.pos,g1.des,g2.pos,g2.des);//desired path and other's path
intersect2 = pathIntersect(g1v.pos,g1v.des,g2.pos,g2.des);//current path and other's path
ctx.strokeStyle = "hsl(30,50%,50%)";
ctx.beginPath();
ctx.moveTo(g1.pos.x,g1.pos.y);
ctx.lineTo(g1.des.x,g1.des.y);
ctx.stroke();
ctx.strokeStyle = "hsl(30,20%,20%)";
ctx.beginPath();
ctx.moveTo(g2.pos.x,g2.pos.y);
ctx.lineTo(g2.des.x,g2.des.y);
ctx.stroke();
if (!intersect) {//
var ratio1 = (1-(1.25*dis/d40))*(1-(1.25*dis/d40));
if (dis/d40 > 0.8) ratio1 = 0;
//account for the angle of direction too...are they heading toward or away from one another?
var ng1 = normalize(guy1.vel);
var ng2 = normalize(guy2.vel);
var ratiod = -(((ng1.vx + ng2.vx) * (ng1.vx + ng2.vx)) + ((ng1.vy + ng2.vy) * (ng1.vy + ng2.vy)))/2 + 1;//between -1 and 1
if (ratiod < 0) ratiod = 0;
ratiod += ratio1;
return {"v":{"vx":v.vx * ratiod,"vy":v.vy * ratiod},
"av":{"vx":av.vx * ratiod,"vy":av.vy * ratiod}};
}
//intersect2 is used to determine who should go first
if (intersect2) {//the current paths also intersect
//number of frames until intersect
var t1 = getDistance(intersect2,g1.pos) / guy1.speed;
var t2 = getDistance(intersect2,g2.pos) / guy2.speed;
} else {
//number of frames until intersect
var t1 = getDistance(intersect,g1.pos) / guy1.speed;
var t2 = getDistance(intersect,g2.pos) / guy2.speed;
//if (t2 > t1 || t1 < 1) return {"v":v,"av":av};
}
//no adjustment if t1 < 1... nearly crossing the path
// guy1 will cross the path first, no adjustment
if (t2 > t1 || t1 < 1) return {"v":v,"av":av};
var ratio = t2/t1;//between 0 and 1
var ratio1 = (1-(1.25*dis/d40))*(1-(1.25*dis/d40));
if (dis/d40 > 0.8) ratio1 = 0;
var ratio2 = 3;// * ((d40 - (t1 * guy1.speed)) / d40 + 1);//should yield ratio between 2 and 4
if (t2 - t1 > 50) ratio2 = ratio2 * (1 - ((t2 - t1 - 50) / 50));
if (ratio2 < 0) ratio2 = 0;
if (t1 > 80) ratio2 = ratio2 * (120-t1)/40;
//another adjustment to help ease the transition once their path is almost crossed
if (t2 < 20 && !intersect2) ratio2 = ratio2 * (t2 / 20) * ratio;
ratio2 += ratio1;
var newv = mirrorVector(vector,v)
var newav = mirrorVector(vector,av);
return {"v":{"vx":newv.vx * ratio2,"vy":newv.vy * ratio2},
"av":{"vx":newav.vx * ratio2,"vy":newav.vy * ratio2}};
}
Helper functions and object constructor...function getDistance(a,b){
//provided the x.y position of two objects, find the distance,
//cx and cy represent the center
if (a.cx && b.cx){
var x = b.cx - a.cx;
var y = b.cy - a.cy;
} else {
var x = b.x - a.x;
var y = b.y - a.y;
}
var d = Math.sqrt((x*x)+(y*y));
return d;
}
///this goes in the constructor for each Obstacles object
this.lookAhead = function(vector){
if (vector) {
var nx = vector.vx * 120 * this.speed + this.pos.cx;
var ny = vector.vy * 120 * this.speed + this.pos.cy;
} else {
var nx = this.vel.vx * 120 + this.pos.cx;
var ny = this.vel.vy * 120 + this.pos.cy;
}
return {"pos":{"x":this.pos.cx,"y":this.pos.cy},"des":{"x":nx,"y":ny}};
//position and destination coordinates
};
There it is. My complete algorithm to avoid obstacles! (Satisfaction not guaranteed).
I intend to make a simple web app to demonstrate with full script available for download. Then I can test it out in extreme circumstances and see how it holds up. For the purposes of the game, there will probably be a maximum of 12 characters on the screen at once.
Stay tuned for a related issue: collision detection! Even with a great avoidance algorithm, collisions are inevitable. And frankly, they make games fun!
.png)


























0 comments: